유한요소법(FEM, Finite Elemints Mechod)은 물체를 유한 개의 요소로 작게 분할하여 각각의 영역에 대해 계산을 해 나가는 수학적 계산방법이다. 모든 연속적인 물체는 무한한 자유도를 가지는데 이러한 복잡한 형식으로는 문제를 해결할 수 없기 때문에 유한요소법을 사용한다.
경계 조건
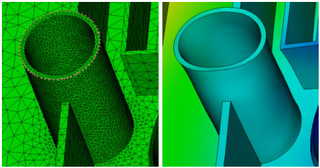
해석을 하기 위해 물체를 대상으로 도형으로 이루어진 경계 조건으로 설정하여 미분 방정식을 푸는 것에서 출발한다. 복잡한 형상의 경계 조건에 대해 미분 방정식을 푸는 것은 대단히 어렵다. 유한요소법의 핵심은 경계 조건을 적용하기 어려운 복잡한 형상 전체를 많은 수의 작고 간단한 도형으로 나누는 것이다. 이 하부 영역의 간단한 도형을 유한요소라고 부른다. 즉 복잡한 형상을 유한 개의 삼각형 또는 사각형과 같은 작은 도형으로 잘게 쪼개서 해석하는 것이다.
자유도를 무한에서 유한으로 전환시키는 도구는 노드(node, 절점)로 연결된 엘리먼트(element, 요소)들의 집합체인 메쉬(mesh, 요소망)이다.
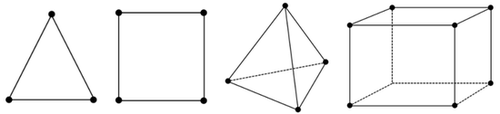
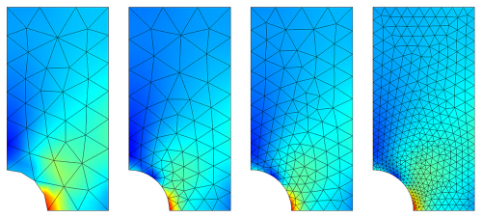
단순한 모양으로 이루어진 작은 도형의 집합은 계산이 간단해지기 때문에 경계 조건을 적용해서 미분 방정식을 이용하는 것이 수월하다. 유한요소의 개수가 많을수록 컴퓨터 연산 시간은 늘어나지만 시뮬레이션의 정확도는 높아진다. 사출성형 유동 해석, 프레스성형 강도 해석 등은 유한요소법을 기반으로 동작하는 분석 기법이다.
해석
해석은 전처리 모델링(pre-processing), 분석(analysis), 후처리 시각화(post-processing)의 3단계로 진행한다. 전처리 모델링에서는 캐드데이터를 불러와서 메쉬를 정의하고 기하학적 도형으로 모델링한다. 3가지 형식의 메쉬 생성 방법이 있는데 목적에 맞게 방식을 선정한다.
빔메쉬(beam mesh, 1D)는 두께 중심 지점(midsurface)을 기준으로 양쪽 방향의 두께 표면을 정의하는 것이고, 셀메쉬(shell mesh, 2D)는 캐드 데이터의 두께 양쪽 면을 이용하는 것이다. 솔리드메쉬(solid mesh, 3D)는 체적을 갖는 모델링 형식이다. 메쉬 모델링 품질은 생성된 연관 결과에 직접 반영된다. 노드 수가 많은 솔리드 방식은 계산 시간이 오래 걸리므로 상황에 맞춰 빔메쉬 또는 셀메쉬를 선호하는 경향이 있다.
메쉬 모델링을 완성하면 성형 재료 종류와 특성 인자를 지정해 준다. 분석 단계에서는 해석을 위한 구속 조건을 설정한다. 사출속도, 사출압력, 수지온도, 금형온도 등의 여러 변수를 입력한다.
후처리 시각화는 해석 결과를 시각적으로 모니터 화면에 보여주는데 수치 눈금, 색상 지도, 등고선 등으로 표현한다.
시뮬레이션 결과에 따라 대상 부품을 수정하고, 수정이 부품 성형에 어떤 영향을 미치게 되는지 확인하기 위해 분석 단계를 재수행하기도 한다. 최종적으로 해석 결과를 바탕으로 목적에 맞는 보고서를 작성하고 금형 설계에 착수한다. 온도, 압력, 수축, 강도 등의 시뮬레이션 결과는 금형설계와 제작 및 사출성형에 필요한 필수적인 엔지니어링 자료이다.